Drehungen um den Ursprung
Bei der Suche nach der Drehmatrix ist es geschickt, die Bildpunkte von P(1|0) und Q(0|1) zu bestimmen. Hier erhält man in Abhängigkeit vom Drehwinkel \alpha: P'(\cos(\alpha)|\sin(\alpha)) und Q'(-\sin(\alpha)|\cos(\alpha)).
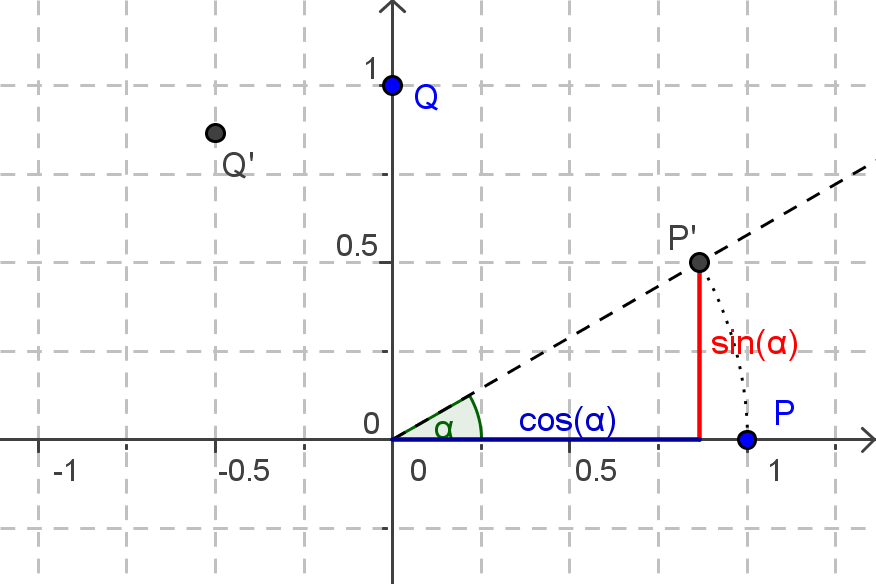
Dies führt wieder zu zwei Bedingungen an die gesuchte Matrix, nämlich: $$ \left(\begin{array}{cc} a&b\\c&d\end{array}\right)\cdot \left(\begin{array}{c} 1\\0\end{array}\right) = \left(\begin{array}{c} \cos(\alpha)\\\sin(\alpha)\end{array}\right)\quad\mbox{und}\quad \left(\begin{array}{cc} a&b\\c&d\end{array}\right)\cdot \left(\begin{array}{c} 0\\1\end{array}\right) = \left(\begin{array}{c} -\sin(\alpha)\\\cos(\alpha)\end{array}\right) $$ Damit erhält man für die Drehmatrix unmittelbar: $$ D_\alpha=\left(\begin{array}{cc} a&b\\c&d\end{array}\right) = \left(\begin{array}{cc} \cos(\alpha)&-\sin(\alpha)\\\sin(\alpha)&cos(\alpha)\end{array}\right) $$
Beispiele:
- \left(\begin{array}{cc} -1&0\\0&-1\end{array}\right) Drehung um 180° (Punktspiegelung)
- \frac{1}{2}\cdot\left(\begin{array}{cc} \sqrt{3}&-1\\1&\sqrt{3}\end{array}\right) Drehung um 30°
- \frac{1}{\sqrt{2}}\cdot\left(\begin{array}{cc} 1&-1\\1&1\end{array}\right) Drehung um 45°
Drehmatrizen und Additionstheoreme
Man kann mit Hilfe von Drehmatrizen leicht die wichtigsten Additionstheoreme für Sinus und Cosinus herleiten. Eine Drehung um den Winkel \alpha+\beta kann man ersetzen durch eine Drehung um den Winkel \alpha und eine anschließende Drehung um den Winkel \beta, also $$ D_{\alpha+\beta}=D_{\beta}\cdot D_{\alpha} $$ Schreibt man die Drehmatrizen in der oben hergeleiteten Form, so erhält man: $$ \left(\begin{array}{cc} \cos(\alpha+\beta)&-\sin(\alpha+\beta)\\\sin(\alpha+\beta)&cos(\alpha+\beta)\end{array}\right)=D_{\alpha+\beta}=D_{\beta}\cdot D_{\alpha} =\left(\begin{array}{cc} \cos(\beta)&-\sin(\beta)\\\sin(\beta)&cos(\beta)\end{array}\right) \cdot \left(\begin{array}{cc} \cos(\alpha)&-\sin(\alpha)\\\sin(\alpha)&cos(\alpha)\end{array}\right) $$ $$ =\left(\begin{array}{cc} \cos(\beta)\cdot\cos(\alpha)-\sin(\beta)\cdot\sin(\alpha)&-\cos(\beta)\cdot\sin(\alpha)-\sin(\beta)\cdot\cos(\alpha)\\\sin(\beta)\cdot\cos(\alpha)+\cos(\beta)\cdot\sin(\alpha)&-\sin(\beta)\cdot\sin(\alpha)+\cos(\beta)\cdot\cos(\alpha)\end{array}\right) $$ Hier liest man unmittelbar zwei Additionstheoreme ab: $$ \sin(\alpha+\beta)=\sin(\alpha)\cdot\cos(\beta)+\sin(\beta)\cdot\cos(\alpha) $$ $$ \cos(\alpha+\beta)=cos(\alpha)\cdot\cos(\beta)-\sin(\alpha)\cdot\sin(\beta) $$