Geometrische Abbildungen
Aufgabe 1 Welche Abbildungen sind das? $$ \mbox{a)}\;\left(\begin{array}{cc}1 &0 \\ 0 & -1 \end{array}\right)\quad \mbox{b)}\;\left(\begin{array}{cc}0 &1 \\ 1 & 0 \end{array}\right)\quad \mbox{c)}\;\left(\begin{array}{cc}0 &1 \\ -1 & 0 \end{array}\right)\quad \mbox{d)}\;\left(\begin{array}{cc}2 &0 \\ 0 & 2 \end{array}\right)\quad \mbox{e)}\;\left(\begin{array}{cc}0 &2 \\ 2 & 0 \end{array}\right)\quad \mbox{f)}\;\left(\begin{array}{cc}1 &0 \\ 0 & 0 \end{array}\right) $$
Aufgabe 2 Ist durch die Matrix eine Spiegelung oder Drehung festgelegt? Bestimme gegebenenfalls die Spiegelachse beziehungsweise den Drehwinkel. $$ \mbox{a)}\;\;\frac{1}{5}\left(\begin{array}{cc}-3 &4 \\ 4& 3 \end{array}\right)\quad \mbox{b)}\;\;\frac{1}{25}\left(\begin{array}{cc}24&7 \\ -7&24 \end{array}\right)\quad \mbox{c)}\;\;\frac{1}{13}\left(\begin{array}{cc}5&12\\12&-5 \end{array}\right)\quad \mbox{d)}\;\;\frac{\sqrt{2}}{2}\left(\begin{array}{cc}-1&-1\\-1&1 \end{array}\right) $$ $$ \mbox{e)}\;\;\frac{1}{2}\left(\begin{array}{cc}\sqrt{3}&1\\-1&\sqrt{3} \end{array}\right)\quad \mbox{f)}\;\;\frac{\sqrt{5}}{5}\left(\begin{array}{cc}-2&-1\\1&-2 \end{array}\right) $$
Aufgabe 3 Wir haben Spiegelmatrizen durch die Steigung m der Spiegelachse beschrieben. Es war $$ S=\frac{1}{1+m^2}\left(\begin{array}{cc}1-m^2&2m \\ 2m&-(1-m^2) \end{array}\right) $$ Beschreibe die Matrix durch den Winkel \varphi, den Spiegelachse mit der x-Achse bildet. (Möglicherweise benötigt man Additionstheoreme)
Aufgabe 4 Aus der Mittelstufe weiß man (möglicherweise), dass man eine Drehung durch zwei Spiegelungen an geeigneten Achsen ersetzen kann. Zeige dies mit Hilfe von Matrizen.
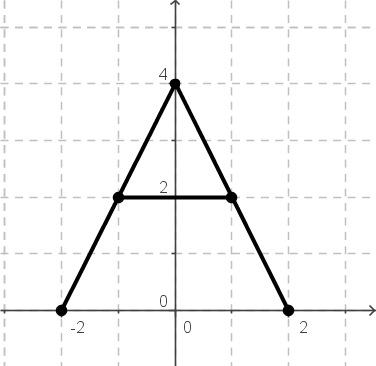
Aufgabe 5 Bilde das nebenstehende "A" ab, d.h. bestimme die Abbildungsmatrix.
- Strecke mit dem Faktor 0,5, drehe dann um 60° und schere anschließend um 30° in Richtung der x-Achse.
- Spiegle an der x-Achse, schere dann um 45° in Richtung der x-Achse und strecke anschließend mit dem Faktor 2.
Spielt die Reihenfolge der Abbildungen eine Rolle?
Aufgabe 6 Wie sieht die Matrix für eine Scherung in Richtung der y-Achse aus? Man kann zwei Wege für die Lösung beschreiten:
- Löse das Problem elementar zu Fuß wie in Abbildungen04
- Führe zuerst eine geeignete Drehung aus, schere dann in Richtung der x-Achse und drehe dann zurück.
Aufgabe 7 Gegeben ist die affine Abbildung $$ \vec{x}\mapsto \frac{1}{2}\left(\begin{array}{cc}1&-\sqrt{3}\\\sqrt{3}&1 \end{array}\right)\cdot \vec{x} + \frac{1}{2}\left(\begin{array}{c}-3+4\sqrt{3}\\4+3\sqrt{3} \end{array}\right) $$ Zeige, dass es sich bei dieser Abbildung um eine Drehung handelt. Bestimme den Drehwinkel und das Drehzentrum.