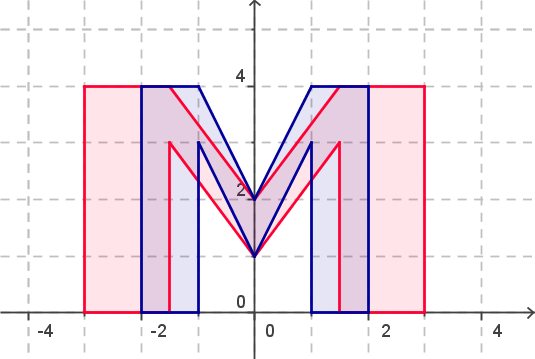
Zentrische Streckungen
Die aus der Mittelstufe bekannte zentrische Streckung lässt sich besonders einfach mit Hilfe von Matrizen realisieren. Eine zentrische Streckung mit dem Streckfaktor k\not= 0 und dem Ursprung als Streckzentrum hat die Matrix $$ \left(\begin{array}{cc} k&0\\0&k\end{array}\right) $$ Beispiele:
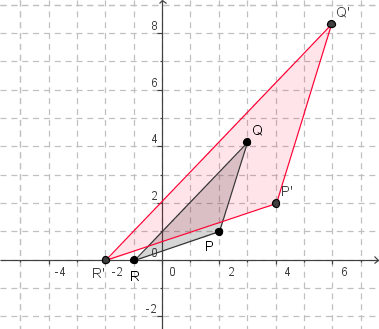
Streckung mit dem Faktor k=2 und Streckung mit dem Faktor k=0{,}6
Es gilt $$ \left(\begin{array}{cc} k&0\\0&k\end{array}\right)\cdot\left(\begin{array}{c} x\\y\end{array}\right)=\left(\begin{array}{c} kx\\ky\end{array}\right)=k\cdot\left(\begin{array}{c} x\\y\end{array}\right) $$ Also kann man eine zentrische Streckung auch einfach als eine Skalarmultiplikation auffassen.
Weitere Streckungen
Eine Matrix der Form \left(\begin{array}{cc} 1&0\\0&k\end{array}\right) streckt von der x-Achse aus in Richtung der y-Achse. Eine Matrix der Form \left(\begin{array}{cc} k&0\\0&1\end{array}\right) streckt in Richtung der x-Achse.
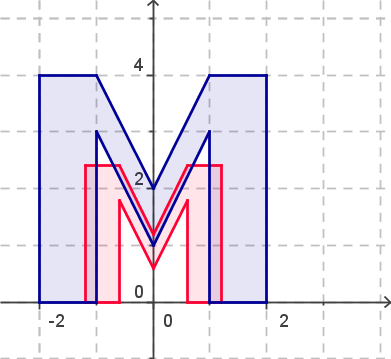
Beispiele: a) Die Matrix \left(\begin{array}{cc} 1&0\\0&\frac{1}{2}\end{array}\right) ergibt die folgende Abbildung:
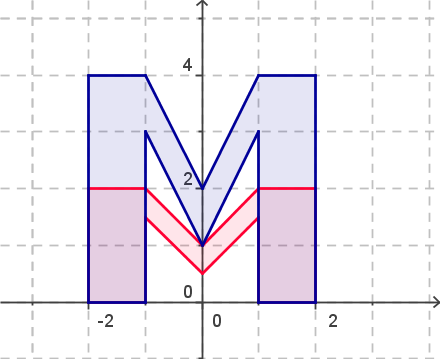
b) Die Matrix \left(\begin{array}{cc} 1{,}5&0\\0&1\end{array}\right) ergibt die folgende Abbildung: