Geometrische Abbildungen II
Aufgabe 1 Welche der folgenden Geraden sind gleich? \[ a:\vec{x}=\left(3\atop 4\right)+t\cdot\left(2\atop 1\right) \] $$ b: 2y=3x+5 $$ $$ c:\vec{x}=\left(1\atop 3\right)+t\cdot\left(-4\atop -2\right) $$ $$ d:\vec{x}=\left(-1\atop 2\right)+t\cdot\left(3\atop 2\right) $$ $$ e: \mbox{Gerade durch die Punkte } P(-3|1) \mbox{und} Q(5|5)$$
Aufgabe 2 Gegeben sind die Geraden: $$ g:\vec{x}=\left(2\atop -4\right)+t\cdot\left(0\atop 2\right) $$ $$ h:\vec{x}=\left(1\atop 3\right)+t\cdot\left(5\atop 1\right) $$ $$ k:\vec{x}=\left(-3\atop 8\right)+t\cdot\left(2\atop -3\right) $$ Bestimme die Schnittpunkte.
Aufgabe 3 Bestimme die Abbildungsvorschrift für die folgenden Abbildungen:
- Drehung um 60° um das Drehzentrum \left( -2\atop 1\right).
- Spiegelung an der Geraden durch die Punkte (0|-2) und(3|3).
Aufgabe 4 Bestimme die affine Abbildung, die das Dreick PQR in der dargestellten Art und Weise abbildet.
a)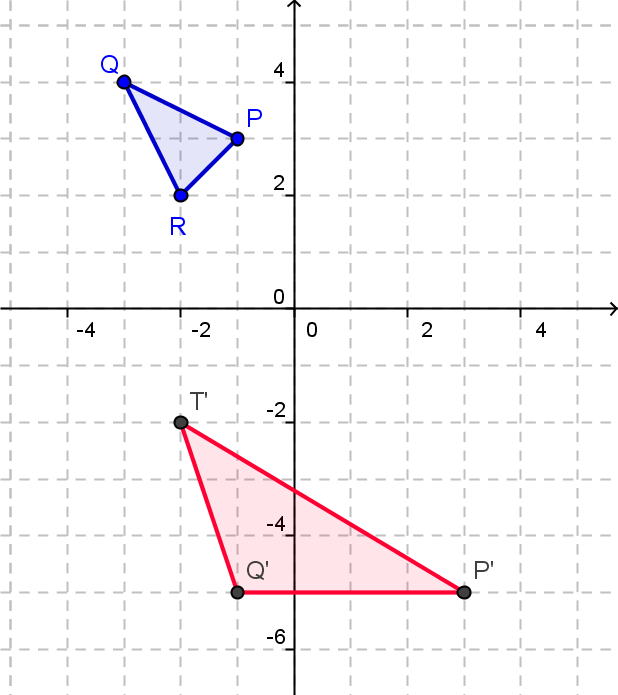 b)
b)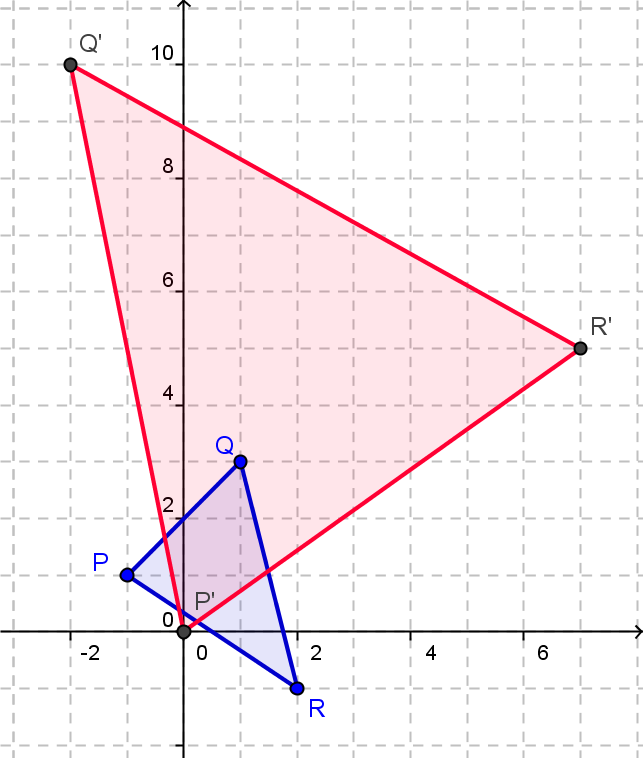
Aufgabe 5 Untersuche die affinen Abbildungen auf Fixelemente. $$ \mbox{a)}\quad A:\vec{x}\mapsto\frac{1}{7}\left( \begin{array}{cc} -2 & 6 \\ 18 & -5 \end{array} \right) \cdot \vec{x} + \left ( \begin{array}{c} 3 \\ -6 \end{array} \right ) $$ $$ \mbox{b)}\quad A:\vec{x}\mapsto\frac{1}{5}\left( \begin{array}{cc} 1 & 3 \\ -2 & 4 \end{array} \right) \cdot \vec{x} + \left ( \begin{array}{c} -3 \\ 2 \end{array} \right ) $$ $$ \mbox{c)}\quad A:\vec{x}\mapsto\pmatrix{-\frac{19}{6} & \frac{11}{3}\cr \frac{11}{6} & -\frac{4}{3}} \cdot \vec{x} + \pmatrix{\frac{97}{6}\cr -\frac{47}{6}} $$ $$ \mbox{d)}\quad A:\vec{x}\mapsto\pmatrix{0 & -1\cr -\frac{1}{2} & \frac{7}{4}} \cdot \vec{x} + \pmatrix{4\cr -\frac{11}{2}} $$ $$ \mbox{e)}\quad A:\vec{x}\mapsto\pmatrix{2 & -\frac{3}{5}\cr -3 & \frac{6}{5}} \cdot \vec{x} + \pmatrix{\frac{1}{5}\cr \frac{13}{5}} $$
Aufgabe 6 Gegeben ist die affine Abbildung
$$ \vec{x}\mapsto\pmatrix{-\frac{1}{5} & \frac{18}{5}\cr \frac{3}{5} & -\frac{4}{5}} \cdot \vec{x} + \pmatrix{-6\cr 3} $$ Bestimme die Bilder der Geraden
$$ g:\vec{x}=\left(-2\atop 1\right)+t\cdot\left(3\atop 1\right) $$ $$ h:\vec{x}=\left(1\atop 3\right)+t\cdot\left(2\atop -3\right) $$ $$ k:\vec{x}=\left(-2\atop 1\right)+t\cdot\left(2\atop -1\right) $$