LineareAlgebra.Abbildungen02 History
Hide minor edits - Show changes to markup
\left(\begin{array}{cc} \frac{1-m^2}{1+m^2}&\frac{2m}{1+m^2}\\\frac{2m}{1+m^2}&-\frac{m^2-1}{1+m^2}\end{array}\right)=
\left(\begin{array}{cc} \frac{1-m^2}{1+m^2}&\frac{2m}{1+m^2}\\\frac{2m}{1+m^2}&\frac{m^2-1}{1+m^2}\end{array}\right)=
\left(\begin{array}{cc} \frac{1-m^2}{1+m^2}&\frac{2m}{1+m^2}\\\frac{2m}{1+m^2}&-\frac{1-m^2}{1+m^2}\end{array}\right)=
\left(\begin{array}{cc} \frac{1-m^2}{1+m^2}&\frac{2m}{1+m^2}\\\frac{2m}{1+m^2}&-\frac{m^2-1}{1+m^2}\end{array}\right)=
S_m\left(\begin{array}{cc} a&b\\c&d\end{array}\right)=
S_m=\left(\begin{array}{cc} a&b\\c&d\end{array}\right)=
- \left(\begin{array}{cc} \frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&-\frac{3}{5}\end{array}\right) Spiegelung an der Geraden y=2x, d.h. m=2
- \left(\begin{array}{cc} -\frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&\frac{3}{5}\end{array}\right) Spiegelung an der Geraden y=2x, d.h. m=2
- \left(\begin{array}{cc} \frac{3}{5}&\frac{4}{5}\\\frac{4}{5}&-\frac{3}{5}\end{array}\right) Spiegelung an der Geraden y=2x, d.h. m=2
- \left(\begin{array}{cc} -1&0\\0&1\end{array}\right) Spiegelung an der y-Achse. Dies kann man mit \lim_{m\rightarrow\infty}S_m bestimmen oder man charakterisiert die Spiegelgerade durch den Winkel mit der x-Achse statt durch die Steigung (siehe Aufgabe 3).
- \left(\begin{array}{cc} -1&0\\0&1\end{array}\right) Spiegelung an der y-Achse. Dies kann man mit \lim_{m\rightarrow\infty}S_m bestimmen oder man charakterisiert die Spiegelgerade durch den Winkel mit der x-Achse statt durch die Steigung (siehe Aufgabe 3).
\left(\begin{array}{cc} a&b\\c&d\end{array}\right)=
S_m\left(\begin{array}{cc} a&b\\c&d\end{array}\right)=
- \left(\begin{array}{cc} 1&0\\0&-1\end{array}\right) Spiegelung an der x-Achse (m=0)
- \left(\begin{array}{cc} 0&1\\1&0\end{array}\right) Spiegelung an der Geraden y=x (m=1)
- \left(\begin{array}{cc} -1&0\\0&1\end{array}\right) Spiegelung an der y-Achse
- \left(\begin{array}{cc} 1&0\\0&-1\end{array}\right) Spiegelung an der x-Achse, d.h. m=0
- \left(\begin{array}{cc} 0&1\\1&0\end{array}\right) Spiegelung an der Geraden y=x, d.h. m=1
- \left(\begin{array}{cc} -1&0\\0&1\end{array}\right) Spiegelung an der y-Achse. Dies kann man mit \lim_{m\rightarrow\infty}S_m bestimmen oder man charakterisiert die Spiegelgerade durch den Winkel mit der x-Achse statt durch die Steigung (siehe Aufgabe 3).
- \left(\begin{array}{cc} 1&0\\0&-1\end{array}\right) Spiegelung an der x-Achse (m=0)
- \left(\begin{array}{cc} 0&1\\1&0\end{array}\right) Spiegelung an der Geraden y=x (m=1)
- \left(\begin{array}{cc} 0&1\\-1&0\end{array}\right) Spiegelung an der $x$-Achse
- \left(\begin{array}{cc} 0&1\\-1&0\end{array}\right) Spiegelung an der Geraden y=x
Beispiele:
- \left(\begin{array}{cc} -1&0\\0&1\end{array}\right) Spiegelung an der y-Achse
- \left(\begin{array}{cc} 0&1\\-1&0\end{array}\right) Spiegelung an der $x$-Achse
- \left(\begin{array}{cc} 0&1\\-1&0\end{array}\right) Spiegelung an der Geraden y=x
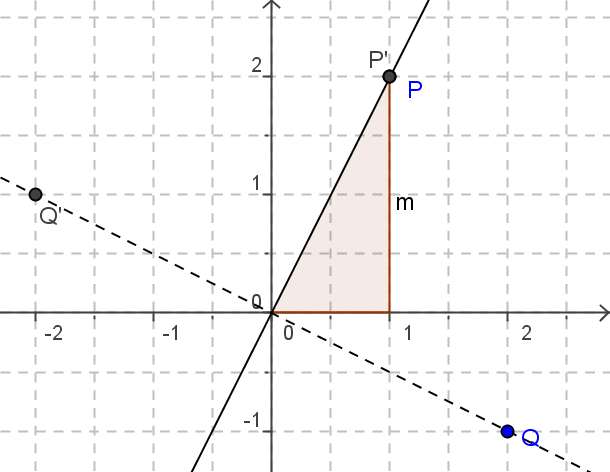
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m) und Q(m|-1). Der Punkt P liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m) und Q(m|-1). Der Punkt P liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bildpunkt von Q ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Spiegelmatrizen
Spiegelungen an Ursprungsgeraden
$$ \left(\begin{array}{cc} a&b\\c&d\end{array}\right)= \left(\begin{array}{cc} \frac{1-m^2}{1+m^2}&\frac{2m}{1+m^2}\\\frac{2m}{1+m^2}&-\frac{1-m^2}{1+m^2}\end{array}\right)= \frac{1}{1+m^2}\left(\begin{array}{cc} 1-m^2&2m\\2m&m^2-1\end{array}\right) $$
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m) und Q(m|-1). P liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m) und Q(m|-1). Der Punkt P liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Dies führt zu zwei Bedingungen an die gesuchte Matrix, nämlich: $$ \left(\begin{array}{cc} a&b\\c&d\end{array}\right)\cdot \left(\begin{array}{c} 1\\m\end{array}\right) = \left(\begin{array}{c} 1\\m\end{array}\right)\quad\mbox{und}\quad \left(\begin{array}{cc} a&b\\c&d\end{array}\right)\cdot \left(\begin{array}{c} m\\-1\end{array}\right) = \left(\begin{array}{c} -m\\1\end{array}\right) $$ Damit kann man die Koeffizienten der Matrix als Lösung der folgenden Gleichungen bestimmen: $$ \begin{array}{ccccc} a&+&bm&=&1\\c&+&dm&=&m\end{array} \qquad\qquad\qquad\qquad\quad \begin{array}{ccccc} am&-&b&=&-m\\cm&-&d&=&1\end{array} $$ Löst man diese Gleichungen, so erhält man die gesuchte Spiegelmatrix in Abhängigkeit von der Steigung m:
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m\/ ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m)\/ und Q(m|-1). P\/ liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q\/ ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m) und Q(m|-1). P liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.
Um die Matrix zu finden, die eine Spiegelung an der Ursprungsgeraden mit Steigung m\/ ist, betrachtet man zwei spezielle Punkte, nämlich P(1|m)\/ und Q(m|-1). P\/ liegt auf der Spiegelachse und wird durch die Spiegelung auf sich selbst abgebildet. Der Bilpunkt von Q\/ ist offenbar Q'(-m|1), denn die Steigung der Normalen ist -\frac{1}{m}.